⚙ 4. 비용 최소화

---

🔨 오늘은 비용최소화 이론에 대해서 알아보자.

---

1. 가설함수 / 비용함수

🔨 Hypothesis

$$H(x) = Wx + b$$

🔨 Cost

$$cost(W,b) = \frac{1}{m}\sum_{i=1}^m(H(x_i) - y_i)^2$$

🔨 비용이 작을수록 우리의 예측이 실제 데이터에 가까움.

• 즉, cost 값이 최소가 되는 $W$와 $b$를 찾는 것이 우리의 목표다🙃!!

2. 간략화한 가설함수

🔨 Hypothesis

$$H(x) = Wx$$
🔨 Cost $$cost(W) = \frac{1}{m}\sum_{i=1}^m(Wx_i - y_i)^2$$

🔨 cost 함수에 예측한 $W$값과 데이터의 $x_i$값, $y_i$값을 대입하면 그 $W$에 대한 비용이 산출됨

• 이 비용을 최소화하는 $W$를 찾자

🔨 프로그램이 비용을 최소화하는 $W$값을 찾는 알고리즘이 Gradient Descent Algorithm (경사하강법)이다.

3. gradient descent algorithm

🔨 경사하강법

• 비용을 최소화하는 알고리즘
• 비용함수의 경사를 따라 내려가면서 최저점을 찾음.
• 최적화 : 손실을 최소화함.
• 변수가 2개 이상인 경우에도 사용하기 좋은 알고리즘이다.

3.1. 과정

---

1. $W,b$ 값을 최초추정함 : 변수값을 임의의 값으로 정해줌
2. 맨 처음의 점에서 비용을 계산한뒤 비용을 줄일 수 있는 방향으로 $W,b$ 값을 업데이트해나감
3. 비용을 줄이는 기울기값과 $W,b$ 값을 얻는 과정을 최솟값에 도달할 때까지 반복함.

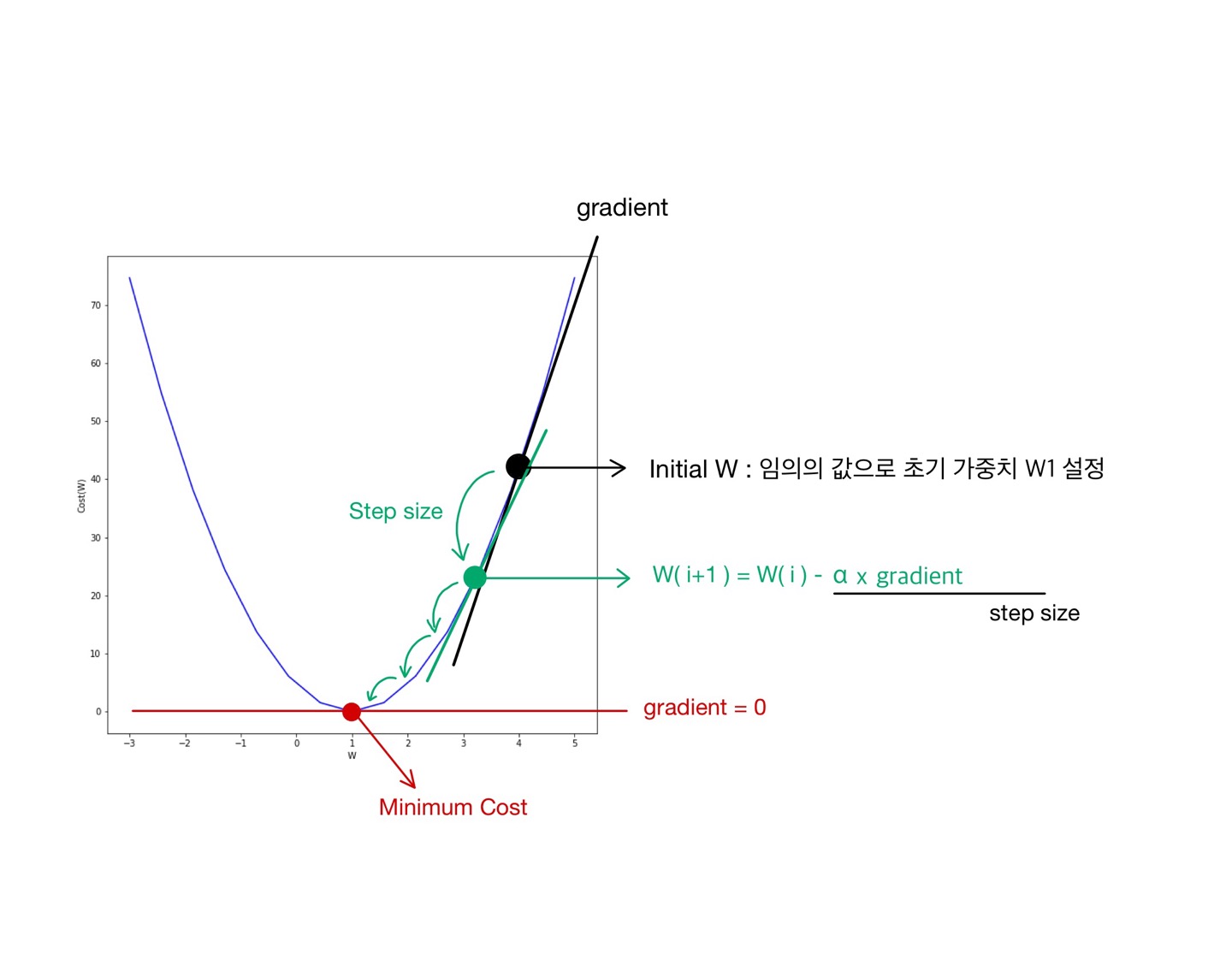
🔨 위의 그림에서 볼 수 있듯이 초기 가중치 $W_0$ 를 설정하고 그 값에서의 gradient를 구해서 $\alpha$ 값을 이용하여 $W_i$ 를 업데이트해준다. 이 과정들을 거쳐서 cost가 최소가 되는 $W$ 값을 찾는다.

• 여기서 $\alpha$는 모델의 학습률을 의미한다. 이 값은 우리가 구한 값을 얼마나 반영해서 학습을 진행할지를 정한다. 주로 작은 값으로 설정해주는 경우가 많다.

3.2. Descent 정의하기

---

🔨 gradient를 구하기 위해서 미분을 하는데 이때 결과값을 간략화하기 위해 형태를 변경해주자.

$$cost(W,b) = \frac{1}{m}\sum_{i=1}^m(H(x_i) - y_i)^2$$

에 대해서 미분을 해주면 뒤의 제곱이 앞으로 나와서 x2형태가 될 것이므로 다음과 같은 조치를 취한다.

$$cost(W,b) = \frac{1}{2m}\sum_{i=1}^m(H(x_i) - y_i)^2$$

분모를 $nm$ 으로 나누어도 전체적인 흐름에 큰 지장은 없다는 전제 하에 진행한다.

🔨 이제는 gradient를 구하기 위해 미분을 해보자.
위에서의 cost 함수를 $W$에 대해 편미분해서 $W$를 업데이트 해주면 다음과 같다.

$$W := W - \alpha \frac{1}{m} \sum_{i=1}^m (Wx_i - y_i) x_i$$

이제 이 수식에 학습률 $\alpha$ 와 $W$ , $b$ 값, 데이터의 $x_i$ , $y_i$ 값을 대입하면 다음 $W$ 값이 업데이트된다.
그 뒤부터는 앞서 말했듯이 cost 함수에 $W$ 값과 $x$,$y$ 데이터 값을 대입해 비용을 구해준다.
이 과정을 반복해서 cost를 최소화하는 $W$ 를 찾는다.

🔨 가설함수를 간략화히지 않고 gradient를 구하려면 cost 함수를 $W$와 $b$에 대해서 따로 편미분해서 $W$와 $b$를 각각 업데이트 해주면 된다🙃.

4. Convex / non-convex function

4.1. Non-Convex function

---

🔨 위 그래프와 같이 주변에서 봤을 때 값이 가장 작은 지점(Local Minimum) 이 여러개 존재하면 전체 데이터에 대해서 가장 낮은 지점으로 갈 것을 보장할 수 없다.

🔨 따라서 이런 경우에는 gradient descent를 사용할 수 없다.

4.2. Convex function

---

🔨 반면 cost 함수가 convex function 이라면 Local Minimum = Global Minimum 이므로 어디서 시작하든지 최저점에 도달한다.

🔨 즉 gradient descent를 사용할 수 있다.

---

🔨 이렇게 해서 단순 선형회귀에 대한 이론을 가볍게 살펴보았다. 다음 포스팅에서는 다중 선형회귀에 대해서 알아보도록 하자.